Suppose we have an undirected graph G representing m roads (edges) connecting n towns (nodes), with edge weights describing the distances along the road in miles. Some of these towns have a bus station (call the number of towns with bus stations b). Each town with a bus station has buses that travel from that town along the roads, and have a one-way range of d miles: every town within d miles of road travel from this town through any number of other towns is reachable. A town is well-connected if it is reachable by bus from at least k towns (including itself, if it has a bus station) for some fixed number k. Given G, the list of b towns with bus stations, d, and k, determine the number of well-connected towns.

All graphs will be given with nodes numbered from 0 to n-1, and edges will be provided in a list. For the above:

n - number of towns in the graph (integer)

m - number of roads in the graph (integer)

d - distance a bus can travel one-way (integer)

k - number of towns in order to consider well-connected (integer)

b - number of towns with bus stations (integer)

Where n > b >= k

You may assume that all edge weights are greater than 0. The graph may not be connected.

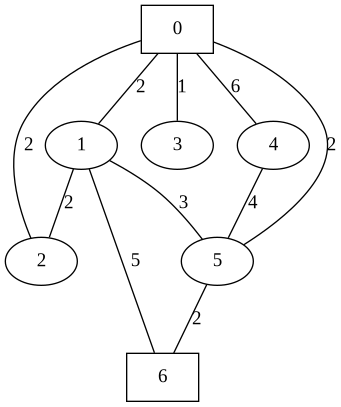
In the above example nodes 0 and 6 are towns with bus stations.

---

Approach

A town is well-connected if at least k towns with bus stations are within a one-way travel distance of d. We can solve this problem using a modified version of BFS similar to Djikstra’s algorithm using a min heap to choose the path with minimal cost. A hashmap is used to keep track of the town and count of how many distinct bus station towns can reach this town {town : n distinct bus stations}. We initialize this algorithm by setting up an adjacency list with inputted edges. Given the nodes of towns of bus stations we iterate through the array and apply our djikstra helper function. In the helper function, the min heap will repeatedly pop the current minimum cost path, increment the respective town’s count of distinct bus stations in the hashmap and append the neighboring towns & accumulate the total distance travel [total current accumulated distance traveled, node]. We repeat this operation until the heap is empty or the accumulated distance is greater than the max distance a bus can travel. We then iterate through the hashmap and increment n_well_connected_towns if the number of bus station towns is greater than or equal to k.

Time Complexity: O(b[(n + m)log(m)])

import heapq

def bfs_helper(starting_node: int, max_distance: int, adj_list: dict, connected_towns_count_map: dict):
    min_heap = [[0, starting_node]]
    visited = set()

    while min_heap:
        current_total_distance, current_node = heapq.heappop(min_heap)

        if current_node in visited:
            continue

        if current_total_distance > max_distance:
            break

        visited.add(current_node)

        connected_towns_count_map[current_node] += 1

        for dst_weight, dst in adj_list[current_node]:
            if dst not in visited:
                heapq.heappush(min_heap, [dst_weight + current_total_distance, dst])


def main():
    n = int(input())
    d = int(input())
    k = int(input())
    b = int(input())
    m = int(input())
    bus_station_nodes = [int(x) for x in input().split()]

    adj_list = {}
    connected_towns_count_map = {}

    for i in range(n):
        adj_list[i] = []
        connected_towns_count_map[i] = 0

    for _ in range(m):
        src, dst, weight = [int(x) for x in input().split()]
        adj_list[src].append([weight, dst])
        adj_list[dst].append([weight, src])

    for node in bus_station_nodes:
        bfs_helper(node, d,
              adj_list, connected_towns_count_map)

    n_well_connected_towns = 0

    for n_stations in connected_towns_count_map.values():
        if n_stations >= k:
            n_well_connected_towns += 1

    print("Number of well connected towns:", n_well_connected_towns)

main()

Test Case

Input:

7
5
2
2
10
0 6
0 1 2
0 2 2
0 3 1
0 4 6
0 5 2
1 2 2
1 5 3
1 6 5
4 5 4
5 6 2

Expected output:

5